コンピューターは0と1で文字や数値を表現したり演算処理を行ったりします。また、二進数の数値を論理回路で演算処理できることは前項で紹介した通りです。二進数の考え方と論理回路を駆使すればコンピューターで大量の計算を高速に処理できます。しかし、一見万能に見えるコンピュータも小数点のある数値を扱うと「0.28-0.27」のような簡単そうな計算でも計算誤差を発生させます。本項では、計算誤差について学習します。
ビットとバイトについて
0と1であらわす二進数のデータ1桁分のことを1bit(ビット)、8桁分のbitを1Byte(バイト)と呼びます。1ビットは2通りの情報しか表せませんが、1Byte(8bit)あれば00000000や11111111の他にも10101010など、全部で256通りの情報を表すことができます。256というのは2を8回かけた数値であり、2の8乗で求められます。
1Byte、つまり256通りあれば、大文字小文字のアルファベットの他に0~9の数値と主要な記号を一通り表現できます。代表的な文字コードであるASCIIコードは1Byteで128通りの文字を表現します。また、かつてはASCIIコードで余った128個分の領域に半角カタカナを追加して、8bitの日本語文字コードとして運用していた時代もありました。
1Byteで数値を扱う場合は56通りなので0~255の数値を表現することが可能です。また、負数を扱う場合は1bit分を正負のフラグとして使うため、-127~+127が表せる数値の範囲となります。
数値は何バイトで表現されるのか?
CPUやOSがサポートするbit幅、また言語などに依存します。初期のパソコンでは8bitや16bitが使われていましたが、1990年代には32bit、2000年代には64bitのCPUがパソコンの主流に変わっていきました。そのため、最近のコンピューターやプログラミング言語では64bitのデータ型は効率よく処理されることを期待できます。
なお、32ビットあれば2の32乗で約42億パターンを表せます。42億あれば漢字や絵文字などを含めた世界中のほとんどの文字を表現可能です。そのため、現在主流の文字コードであるUTF-8は基本的に4Byteを上限として文字を表現しています。
整数を二進数で扱う方法
二進数のビット列を、それぞれの桁数で2nして足し合わせれば表現できます。仮に8bitなら以下のように表せます。
7 = 00001111 = 22 + 21 + 20 = 4 + 2 + 1
となります。
-7も1桁分を負数のフラグにするだけなので10001111と表せます。
小数点がある数値をどのように扱うか?
整数は十分なビット幅があれば二進数に変換しても演算処理できそうですが、小数点のある数値は一筋縄ではいきません。まず、単純な方法として、表現できる数値の桁数は小さくなるけれども誤差の出にくい方法として「固定小数点数」というやり方があります。例えば32bitで±21億を表現できるものを下4桁分、固定で小数に充ててしまえば、約-210,000.0000~+210,000.0000を表現できます。
なお、固定小数点数の方式は扱える桁数が少なくなるため、お金の計算など誤差が許されないプログラムでは使われますが、基本的には「浮動小数点数」という仕組みを利用しています。浮動小数点数は扱う値ごとに小数点の位置が浮動のため、小数が扱えるだけでなく同じビット数で整数型よりも大きい数値を表すこともできます。ただし、「計算誤差」が発生するようになります。
JavaScriptはどのようなデータ型で数値を扱っているのか?
プログラミング言語によっては変数を宣言するときにデータ型を指定しますが、JavaScriptでは代入時に動的にデータ型が決まります。また、数値は全てdouble型(64bit)となります。
JavaScriptのdouble型は整数としては53bit分の値を安全に扱えます。
具体的には以下の値となります。
9007199254740991
JavaScript上で定数「Number.MAX_SAFE_INTEGER」を参照すれば上記の値を確認できます。とにかく、9000兆(16桁)までは扱えるようです。9000兆というのは世界の時価総額に匹敵するようです。
また、double型は浮動小数点数としても機能します、その場合は下記の値まで表現できます。
1.7976931348623157 x 10308
10の308乗という途方もない桁数(つまり308桁)の値を扱えます。
桁あふれのサンプルプログラム
double型で扱える数値を以下のプログラムで確認してみましょう。
<script>
x = 1.7976931348623157e+308;
document.writeln(x+"<br>"); // 17976931348623157がdoble型で表せる数値の桁的な上限
x = 1.7976931348623157 * 10 ** 308;
document.writeln(x+"<br>"); // e+308というのは10の308乗という意味
x = 1.797693134862315799999e+308;
document.writeln(x+"<br>"); // 1.797693134862315799999は表せないので桁が切り捨てられる
x = 1.797693134862315799999e+307;
document.writeln(x+"<br>"); // 10の307乗に減らしても1.797693134862315799999は表せない
x = 1.7976931348623157e+309;
document.writeln(x+"<br>"); // 10の309乗するとオーバーフローして無限になる
x = 1.8e+308;
document.writeln(x+"<br>"); // 1.8 * 10の308乗もオーバーフローして無限になる
x = -1.8e+307;
document.writeln(x+"<br>"); // 1.8 * 10の307乗ならオーバーフローはしない
</script>
実行結果
1.7976931348623157e+308
1.7976931348623157e+308
1.7976931348623157e+308
1.7976931348623158e+307
Infinity
Infinity
-1.8e+307
解説
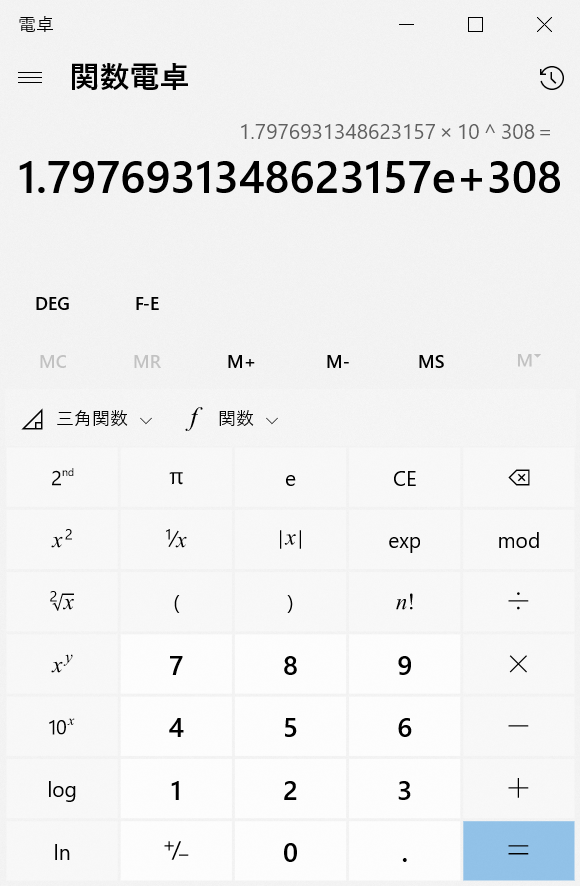
プログラム中のコメントの通りですが、1.7976931348623157e+308のe+308というのは10の308乗という意味です(10308)。なので、「1.7976931348623157 * 10 ** 308」(**はべき乗、10 ** 308は(10308という意味)と計算しても出力結果は1.7976931348623157e+308と表記されます。これはいわゆる指数表記なわけです。関数電卓で同じ計算をさせても、同じ指数表記になります。
また、double型では「1.7976931348623157e+308」までは浮動小数点数として扱えるのですが、「1.79769313486231579999e+308」みたいに、扱える上限を超えて桁が増えると切り捨てられて「1.7976931348623157e+308」までしか表現できません。「1.797693134862315799999e+307」のように乗数の部分を308から307に減らしても、やはり99999の部分は切り捨てられます。
そして「1.7976931348623157e+309」のように乗数の部分をe+309にするとdouble型の上限を超えてInfinityという値になります。また、1.8e+308とした場合も同様です。
計算誤差のサンプルプログラム
<script>
x = 28-27;
document.write(x+"
");
y = 0.28-0.27;
document.write(y+"
")
</script>
実行結果
1
0.010000000000000009
解説
「28-27」は整数同士の計算のため、誤差なく1が演算されます。しかし「0.28-0.27」は浮動小数点数同士の計算のため、精度が犠牲になり計算誤差が発生します。解決方法としては、一度整数に直してから計算して再度、小数に戻す方法などが考えられます。
整数に直す例
最初から整数である必要があります。
<script>
y = ((0.28 * 100) - (0.27 * 100)) / 100;
document.write(y+"
")
y = (28 - 27) / 100;
document.write(y+"
")
</script>
実行結果
(0.28 * 100)の時点ですでに計算誤差がでているため、((0.28 * 100) – (0.27 * 100)) / 100は期待通りの結果にはなりません。
0.010000000000000035
0.01
