文部科学省発行「高等学校情報科『情報Ⅰ』教員研修用教材」の「学習11」にある「コンピュータの仕組み」では論理演算と二進数の足し算が紹介されています。こちらの内容をブラウザで動作するJavaScript製の論理回路シミュレーターSimcirJSで学習する方法を紹介いたします。
はじめに
コンピューターの心臓部であるCPUの内部には膨大な数のトランジスタが集積されています。CPUはトランジスタで論理回路を組むことにより、0と1のデジタル信号を高速に処理して演算処理を行っています。逆に言えば、1+1=2のような単純な10進数の足し算を行う場合でも、2進数のデジタル信号に置き換えて論理回路を通さなければコンピューターは計算を行えません。そこで、コンピュータの仕組みを理解するために論理演算を学習してみましょう。
代表的な論理回路
- AND回路：入力信号がすべて1のときに1を出力します
- OR回路：入力信号が1つでも1ならば1を出力します
- NOT回路：入力信号が0なら1を出力、1ならば0を出力します
論理回路シミュレーター
論理演算や論理回路が実際はどのように動作するかをシミュレーターで確認することができます。
ブラウザ上で動作する論理回路シミュレーター(SimcirJS)
ANDのベン図
ANDの真理値表
| 入力A | 入力B | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
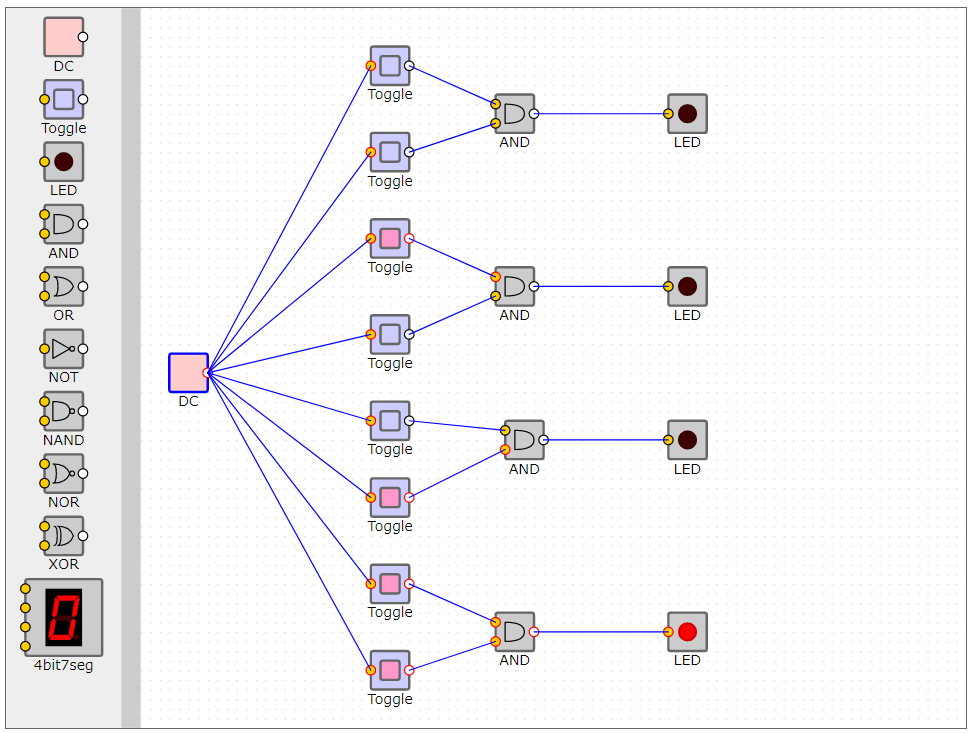
論理回路
ORのベン図
ORの真理値表
| 入力A | 入力B | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
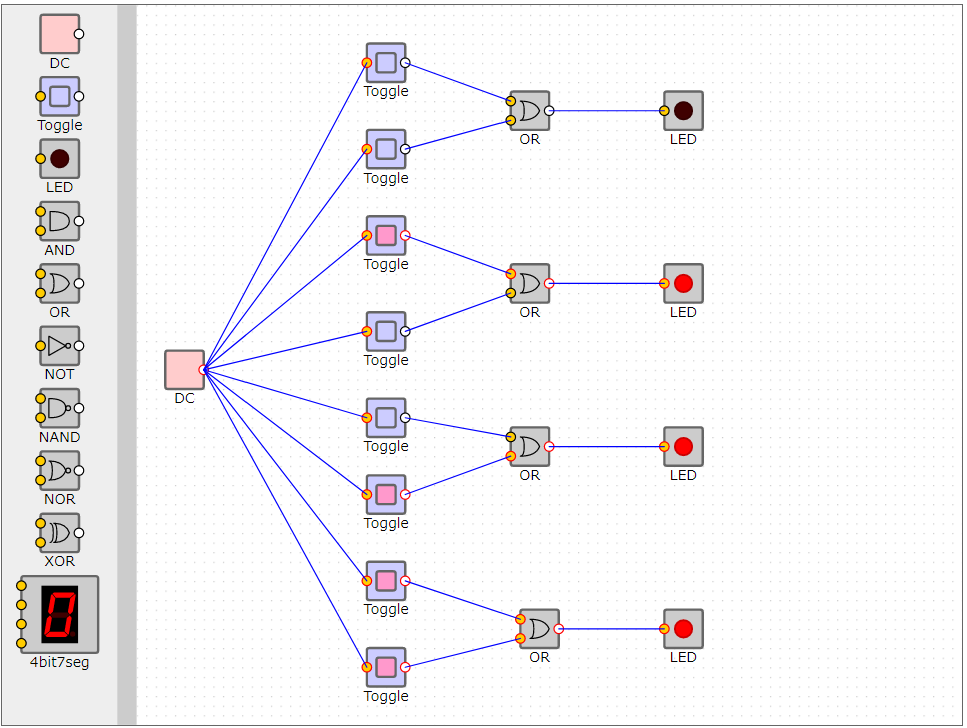
ORの論理回路
NOTのベン図
NOTの真理値表
| 入力 | 出力 |
|---|---|
| 0 | 1 |
| 1 | 0 |
演習：次のベン図と表を描いて下さい
- ANDのベン図の領域を反転させたベン図(NAND)
- ORのベン図の領域を反転させたベン図(NOR)
- AとBが両方1ならば0、AかBが0でも0、AとBのどちらか一方だけが1のときだけ1になるベン図(XOR)
NANDのベン図
NANDの真理値表
| 入力A | 入力B | 出力 |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
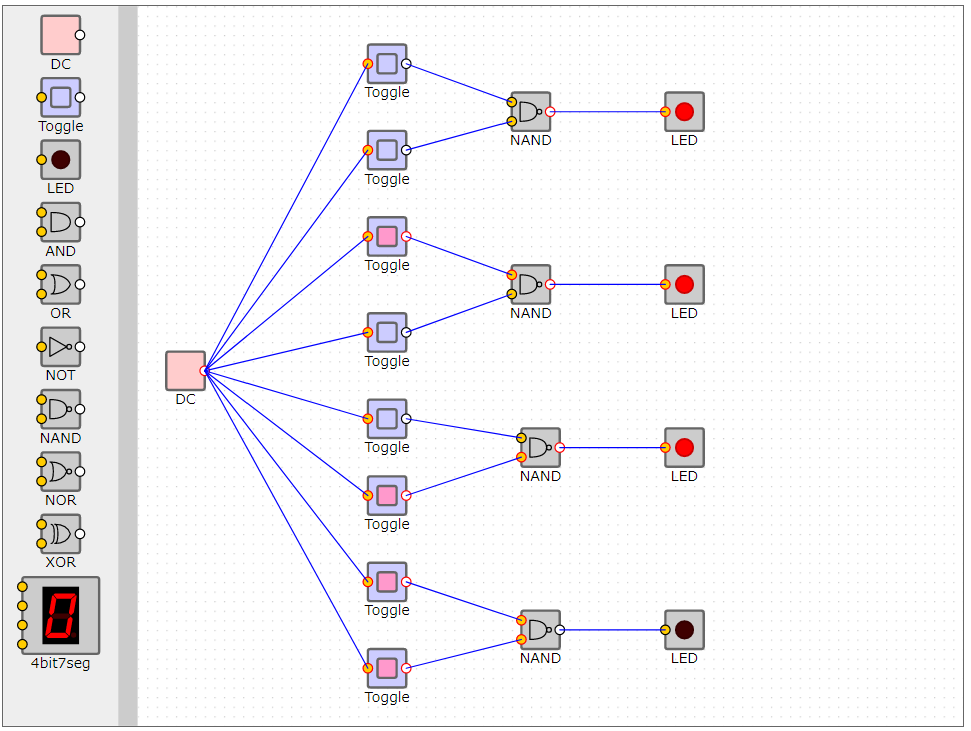
NAND回路
NORのベン図
NORの真理値表
| 入力A | 入力B | 出力 |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
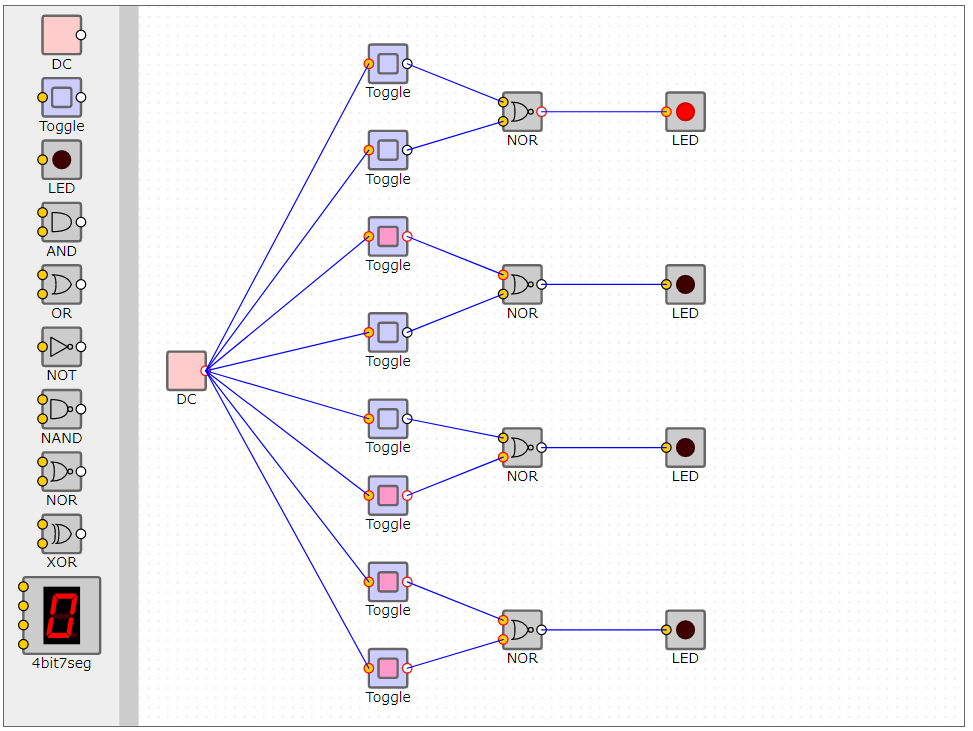
NOR回路
XORのベン図
XORの真理値表
| 入力A | 入力B | 出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
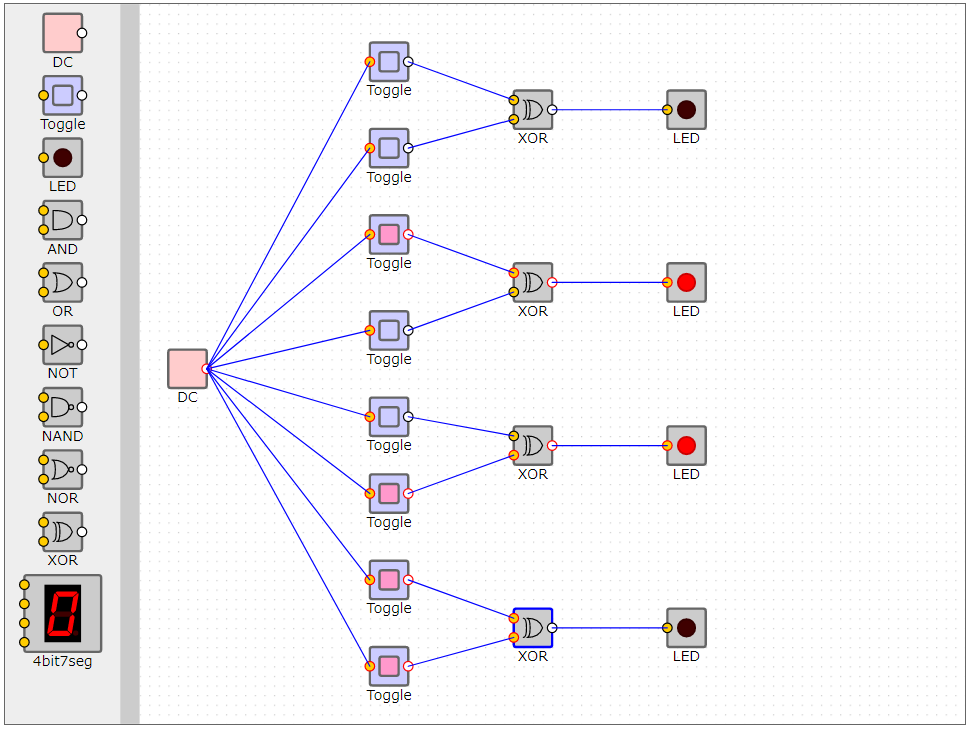
XORの論理回路
論理演算を用いた二進数の足し算
論理回路を組み合わせることで四則演算を行うことができます。今回は二進数の足し算に挑戦します。以下のような回路の空欄を埋めて、2進数の足し算の真理値表を成立させるような回路を組み立てて下さい。
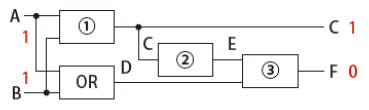
※ 高等学校情報科「情報 」教員研修用教材 JavaScript 版 p.6
2進数の足し算の真理値表
| 入力A | 入力B | 途中経過C | 途中経過D | 出力C | 出力F |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 |
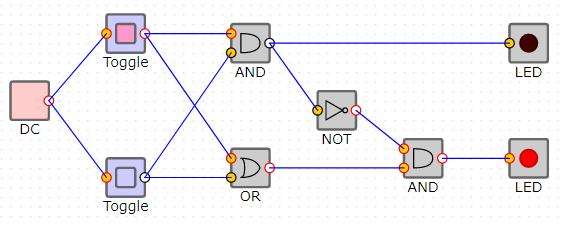
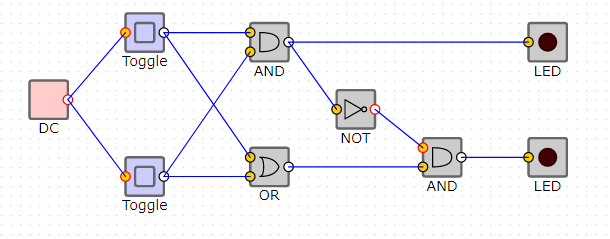
二進数の足し算の論理回路図
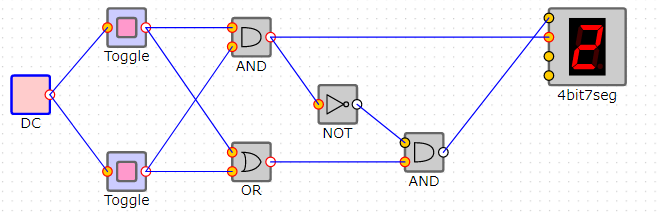
完成形は以下の通りです、AとBが0ならばCもFも0になります。
AもしくはBが1ならば、Cは0、Fは1になります。
AとBが両方1ならば、Cは1、Fは0になります。
7セグメントディスプレイによる16進数での確認
2進数の信号を16進数で表示してくれる7セグメントディスプレイという部品がありますので、上記の回路の出力を渡してみることにします。
はい、1+1は2になりました。
おまけ：論理回路でメモリを実現する方法
論理回路を組み合わせると四則演算が行えることを先ほど確認しました。CPUの中には値を記録するレジスタという仕組みも備わっていますが、こちらも論理回路の組み合わせで実現できます。参考までに回路を掲載します。
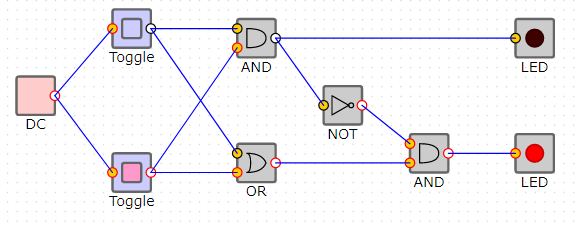
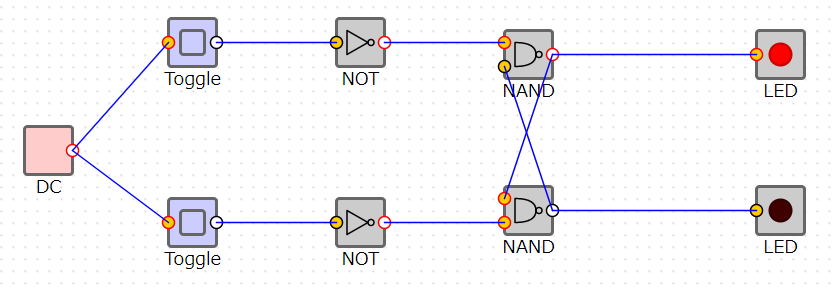
フリップフロップ回路による値の保持
NAND回路が2つあり、お互いの出力をお互いの入力に入れているという不思議な回路です。現在、入力が0,0に対して出力が1,0になっていることを覚えておいて下さい。
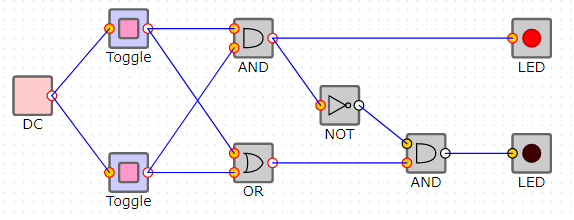
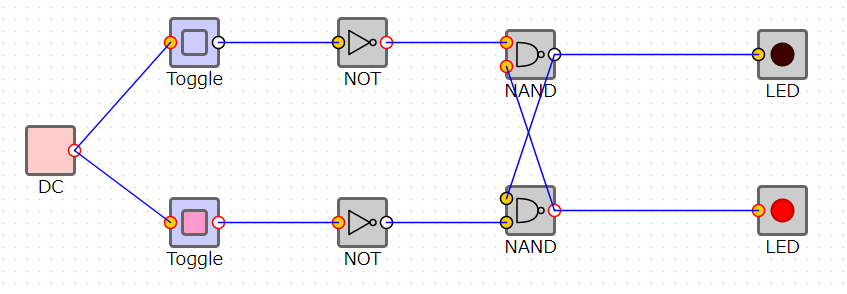
入力を0,1したら出力も0,1になりました。今度は再び、入力を0,0に戻します。
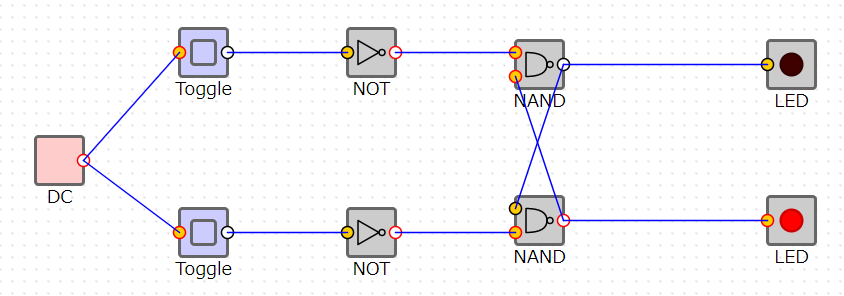
入力が0,0に対して、なんと出力が0,1になっています、というか、0,0に切り替える前の値を保持しています。これがフリップフロップによるメモリの仕組みです。なお、1,1は使いません。
フリップフロップの真理値表
| 入力A | 入力B | 出力C | 出力D |
|---|---|---|---|
| 0 | 0 | 保持 | 保持 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | – | – |