「誤った情報を、訂正するのにかかる時間」をシミュレーションしてみよう
ファクトチェック(事実かどうかチェックする)
インターネット上のソーシャルメディアでは、日々、大量の情報がやりとりされています。大量の情報の中には、誤った情報や、悪意を持って流された情報もまぎれこんでいます。
友達どうしでつながったSNSでも、間違った情報が流れることがあるでしょう。そうやってSNSに流れた間違った情報は、友達との関係を悪化させることがあるかもしれません。

現実の社会でも、誤った情報が悪影響を及ぼすことも少なくありません。
そこで、流通している情報が事実かどうか確認し、誤った情報を見つけた場合には訂正する情報を発する活動が行われています。これをファクトチェック(fact check)といいます。今、様々な組織が、ファクトチェックに取り組んでいます。

特定の分野の専門家が、自分の専門分野に関して誤った情報を見つけたときに、ファクトチェックを行い、訂正する情報を公開するケースも見られます。
誤った情報がなかなか無くならないのはなぜ?
組織や専門家によって、様々な形でファクトチェックが行われ、訂正情報が発せられたとしても、一度広まった誤った情報は、なかなか完全に消えてなくなりません。おかしな噂が、なかなか消えないのと似ています。
これは、「誤った情報」に、「増える」性質があるから、と考えると説明できそうです。
訂正によって「減らす」力が働きますが、「増える」力と「減る」力の両方が働くことで、「全体としては、なかなか消えない」という性質が生まれる、というわけです。
「誤った情報」が、なかなか減らない・無くならないことを理解するために、モデルを使ったシミュレーションをしてみましょう。
捕食・被食関係の数理モデル
今回は、捕食・被食関係を説明する数理モデル「ロトカ・ヴォルテラの方程式」を用います。

このモデルは、ある環境の中の「食べられる者(被食者)」の数と、「食べる者(捕食者)」の数を説明することを目指しています。
実際の環境には、多種多様な生き物がいます。それにも関わらず、捕食者と被食者の、たったの2種類だけで考えるこのモデルは、非常に単純化しています。
ですが、単純だからこそ簡単にシミュレーションに利用できますし、今回のように別の分野に応用することもできます。
ロトカ・ヴォルテラの方程式
数理モデル「ロトカ・ヴォルテラの方程式」とは、次の2つの式のことです。
被食者の数の変化量=aX-bXY
被食者の数の変化量=cXY-dY
いきなりX,Yおよびa,b,c,dと、記号が出てきましたが、それぞれの記号の意味は次の通りです。
| X | 被食者(食べられる者)の現在の数 |
| Y | 捕食者(食べる者)の現在の数 |
| a | 被食者(食べられる者)が増える率。被食者(食べられる者)の現在の数(X)にaを掛けると(aX)、次にどれだけの食べられる者の数が増えるか決まる。 |
| b | 被食者(食べられる者)が減る率。食べられる者の数(X)、食べる者の数(Y)に、bをかけると(bXY)、次にどれだけ食べられる者の数が減るか決まる。
被食者の減り方は、被食者の数と捕食者の数の両方から影響を受ける。 |
| c | 捕食者(食べる者)が増える率。捕食者(食べる者)の現在の数(Y)と被食者(食べられる者)をかけ、さらにcをかけると(cXY)、捕食者(食べる者)の増える量になる。
捕食者の増え方は、被食者の数と捕食者の数の両方から影響を受ける。 |
| d | 捕食者(食べる者)が減る率。捕食者(食べる者)の現在の数(Y)にdをかけると(dY)、次にどれだけ食べる者の数が減るか決まる。 |
1つ目の式の「aX – bXY」とは、「食べられる者の増える量-食べられる者の減る量」という意味になります。式全体の意味を言葉にするなら、「食べられる者の増減量」(※上の1つ目の式の左辺と同じ意味)ということです。
なお、bXYの方がaXより大きければ、全体はマイナスになることを確認しておきましょう。
また、2つ目の式の「cXY – dY」とは、「食べる者の増える量-食べる者の減る量」という意味になります。式全体の意味を言葉にするなら、「食べる者の増減量」(※2つ目の式の左辺と同じ意味)ということです。
こちらも、dYの方がcXYより大きければ、全体はマイナスになることを確認しておきましょう。
最後にもう一度、一歩引いて方程式を見直してみましょう。
被食者の数の変化量=aX-bXY
被食者の数の変化量=cXY-dY
1つ目の式は、「被食者の増え方(aX)は、被食者の今の数次第。一方、減り方(bXY)は、被食者の数と捕食者の数の両方から影響を受ける」と言っています。
2つ目の式は、「捕食者の増え方(cXY)は、捕食者の数と被食者の数の両方から影響を受ける。一方、減り方(dY)は、捕食者の今の数次第」と言っています。
表計算ソフトを使ってシミュレーションする
表計算ソフトを使って、「誤った情報」の量と、「ファクトチェックの情報」の量がどう変化するか、シミュレーションしてみましょう。
ロトカ・ヴォルテラの方程式は増減量を表す式です。現在の量に、方程式の増減量を加えることで、次の世代の量を計算できます。
次の世代のX = X + (aX – bXY)
次の世代のY = Y + (cXY – dY)
※右辺に出てくるX,Yは、いずれも現在のX,Yの値です。X+(Xの変化量)、Y+(Yの変化量)になっています。この計算結果は、それぞれ次の世代のX,Yになります。
方程式に出てくる値は、シミュレーションするときに与える値(※パラメータといいます)になります。
| X | 「ソーシャルメディア上の誤った情報」の最初の量
(※被食者(食べられる者)の現在の数) |
| Y | 「ファクトチェック」の最初の量
(※捕食者(食べる者)の現在の数) |
| a | Xにaを掛けた値が「ソーシャルメディア上の誤った情報の増え方」を表す
(※被食者(食べられる者)が増える率)。 |
| b | X×Yにbを掛けた値が「ソーシャルメディア上の誤った情報の減り方」を表す
(※被食者(食べられる者)が減る率)。 「誤った情報」の減り方は、「誤った情報」の量と、「ファクトチェックの情報」の量の両方から影響を受ける。 |
| c | X×Yにcを掛けた値が「ファクトチェックの増え方」を表す
(※捕食者(食べる者)が増える率)。 「ファクトチェックの情報」の増え方は、「誤った情報」の量と、「ファクトチェックの情報」の量の両方から影響を受ける。 |
| d | Yにdを掛けた値が「ファクトチェックの減り方」を表す
(※捕食者(食べる者)が減る率)。 |
表計算ソフトのシートに、上の6つのパラメータを入れるセルを用意します。また、計算式を入力した表を用意します。
下のリンクから、6つのパラメータを設定して30世代の変化をシミュレーションするExcelファイルをダウンロードできます。
ファイルはZip形式で圧縮してありますので、ダウンロードした上で解凍して利用してください。
ファイルには、あらかじめ次の値でX,Y,a,b,c,dのパラメータを設定済みです。
| X | 100 | 「ソーシャルメディア上の誤った情報」の最初の量
(※被食者(食べられる者)の現在の数) |
| Y | 10 | 「ファクトチェック」の最初の量
(※捕食者(食べる者)の現在の数) |
| a | 0.1 | Xにaを掛けた値が「ソーシャルメディア上の誤った情報の増え方」を表す
(※被食者(食べられる者)が増える率) |
| b | 0.02 | X×Yにbを掛けた値が「ソーシャルメディア上の誤った情報の減り方」を表す
(※被食者(食べられる者)が減る率) |
| c | 0.01 | X×Yにcを掛けた値が「ファクトチェックの増え方」を表す
(※捕食者(食べる者)が増える率) |
| d | 0.3 | Yにdを掛けた値が「ファクトチェックの減り方」を表す
(※捕食者(食べる者)が減る率) |
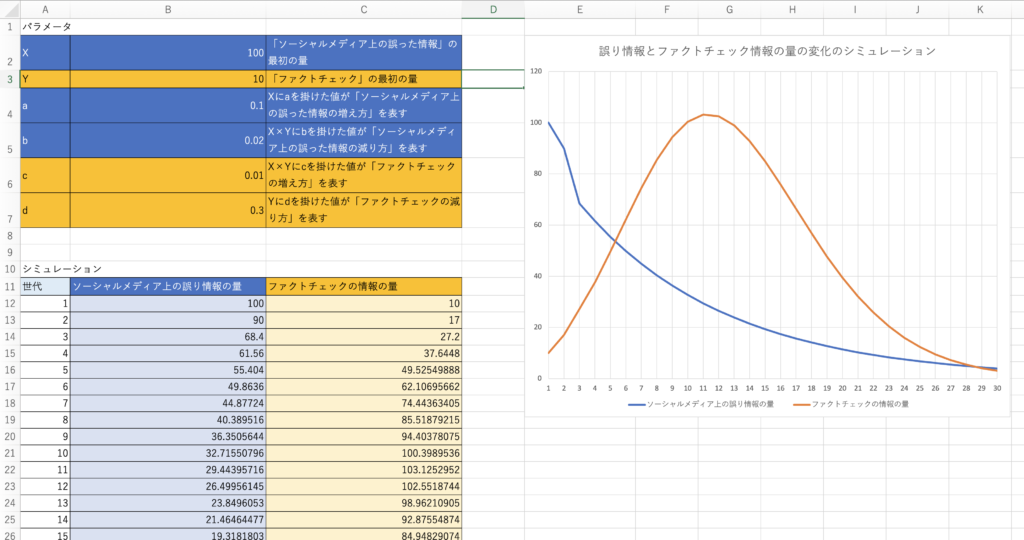
Excelファイルのシートの、パラメータの表の下に、最初の状態から30世代に渡って、その数がどうなるかシミュレーションを行う表を記載しています。表の中の各セルには、前の世代のX、Yの値と、パラメータa,b,c,dの値を参照して計算を行う計算式が仕込まれています。
また、パラメータの表の右には、シミュレーションの結果を表す折れ線グラフがあります。

ダウンロードしたファイルのグラフを見ると、次のようなことが読み取れます。
- 誤り情報は、緩やかに減少していく。
- ファクトチェックの情報は、急速に増えて、6世代目で誤り情報の量を超える。
- 11世代あたりでファクトチェック情報の量が頂点を迎え、そこから急速に減る。
- 29世代目あたりで、誤り情報の量が、少しだけファクトチェック情報の量を上回る。
パラメータの値を変更して、シミュレーションしてみよう
Excelファイルのパラメータの値を変更すると、シミュレーションの結果の表が更新されます。同時に、グラフも更新されます。
ファイルの中の元のシートをコピーして、同じ表・グラフが記載されたシートを作りましょう。そうしてコピーしたシート上のパラメータを変更して、シミュレーションを行い、結果を観察し、考察してみてください。
なお、シミュレーションを行う際は、パラメータを1つずつ変更するようにし、1つ変更するごとに結果を考察することをお勧めします。一度にパラメータを複数変更すると、どのパラメータの効果で結果が変わったか分かりにくくなるからです。
シミュレーションの例
2つのシミュレーション例を紹介します。
【シミュレーション例①】最初の時点の誤り情報が10倍多いとき
パラメータXの値を10倍(=1000)にしてみました。

速やかにファクトチェックが増え、誤り情報が減ったあと、15世代目あたりから10世代ほどにわたって、ファクトチェックの情報の量が激しく増減しています。
実際のところ、情報の「量」はマイナスの値を取らないはずなので、意味を読み取るのが難しいシミュレーション結果です。
ちょっと無理をして解釈するなら、「正しい情報が十分に広まったあと、しばらくするとその情報が失われる(SNSなどで見られなくなる、人々の頭の中から忘れられる)ことがある」と考えることができるかもしれません。
【シミュレーション例②】最初の時点のファクトチェック情報が10分の1のとき
パラメータYの値を10分の1(=1)にしてみました。
グラフの形状が大きく変わっています。

グラフでは、2つの量の関係がどうなったか分かりにくいので、表の方を見てみます。すると、9世代目で逆転が起きていることが分かります。

また、ファクトチェック情報の急激な増加のために、上のグラフでは分かりにくくなっていますが、下のように「誤り情報の量」だけで折れ線グラフを作るとわかる通り、
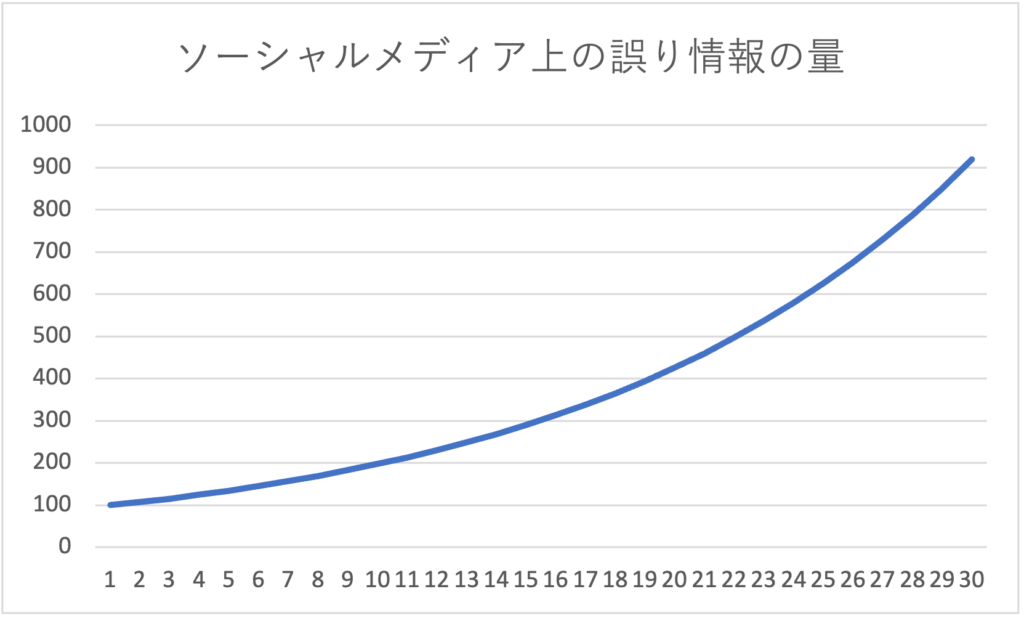
誤り情報は、30世代の間を通じて、全く減少していません。むしろ緩やかに(徐々に加速しながら)増え続けています。
まとめると、「最初の時点で、誤り情報の量がファクトチェックの情報より多い(※この例では、100倍多い)と、早期にファクトチェック情報は誤り情報を上回って増えるにも関わらず、誤り情報は減らずに増え続ける。短期間ではゼロにはならない」ということになります。
特に「短期間では誤り情報はゼロにならない」という部分は、なかなか深刻な推論が出てきたと言えそうです。「誤り情報を訂正する発信源は、早い段階から、多い方がいい」という教訓を導き出しても良いかもしれません。
まとめ
この記事では、「ソーシャルメディア上の誤った情報が、なかなか完全には無くならないのはなぜか」を考えるため、生き物の増減のモデルを応用して、シミュレーションを行いました。
元々のモデル自体、自然現象を単純化しています。それを別の問題に適用しているので、完全に現象を説明しているとは言えないでしょう。
ですが、複雑な現象の1つの側面を捉えて、問題の解決策を考えるためのヒントを得ることができます。シミュレーションを行う意味が、ここにあります。


