ボールの弾みをシミュレーションする
ボールの弾み(跳ね返り)をシミュレーションする
ボールを高いところから落とすと、徐々に加速しながら落ちていきます。そして地面に当たると跳ね返ります。
跳ね返ると、今度は上昇していきますが、徐々に減速して、あるタイミングで上昇を止め(上向きだった速度が0になる)、そこから下降に転じます。また下向きに加速しながら落ちていきます。
以後、下降・着地して跳ね返り・上昇、また下降…を繰り返しますが、無限に繰り返すわけではありません。跳ね返るごとに、到達できる最高地点が下がっていき、最後には全く跳ね返らなくなります。
地面に着地して、跳ね返るときの跳ね返りの強さによって、一連の運動の様子は変わります。
「跳ね返りの強さ」(※アプリでは、反発係数と呼んでいます)を指定できるプログラムを使って、運動の様子を見てみましょう。
サンプルアプリの動作
このアプリでは、同時に3つのボールを落として、動作を確認することができます。3つのボールそれぞれに、反発係数を「0以上1以下」の範囲で指定できます。
3つの反発係数を決めた後、「シミュレーション開始」ボタンをクリックすると、シミュレーションが始まります。
「画面上が地面の上側で、画面下に地面がある」という想定です。ボールは画面左上から、右に向かって投げられたかのように動きます。
後からボールの動きを追跡・確認できるように、円の動きの軌跡を線で示します。
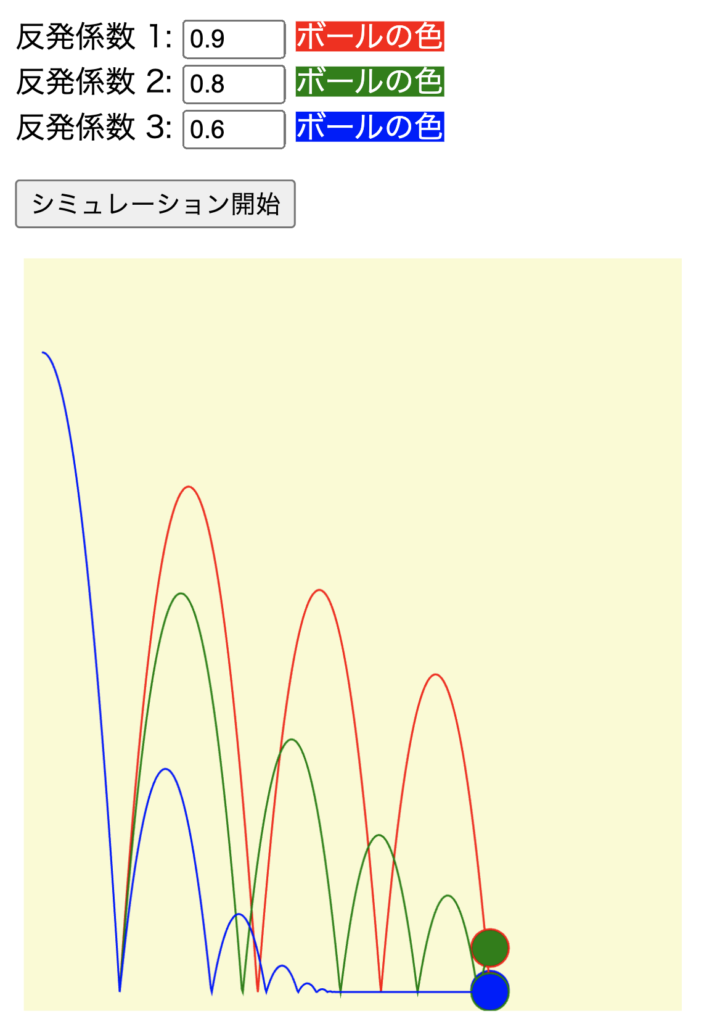
このアプリは、全てのボールが3回弾んだ後、4回目に地面に当たったところで停止します。
さまざまに反発係数を変更して、運動の様子を見てみましょう。
アプリとソースコードのインポート
以下のボタンをクリックすると、Monaca Educationにプロジェクトをインポートできます。
Monaca Educationにインポートする(要ログイン)
このプログラムは、JavaScriptのライブラリp5.jsを使って作成しました。p5.jsは、Processingというプログラミング言語・環境の特徴をJavaScriptに持ち込んだものです。今回の作例のように、プログラミングをして、アニメーションを作ることができます。
計算の誤差
今回紹介したアプリで、跳ね返りの強さを1にすると、どうなるでしょうか。
本来なら、ボールを離した元の高さ(初めの高さ)まで戻り、無限に繰り返します。
しかし、このサンプルプログラムでは、最高地点が変動する様子が観察できます。これは、ボールの位置やボールの移動速度(落下・上昇の速度)を計算するときに、小数を含む演算を繰り返し行っていて、誤差が生じるためです。
厳密なシミュレーションを行う場合には、コンピュータによる計算ならではの誤差を防ぐために工夫が必要になります。


