文部科学省発行「高等学校情報科『情報Ⅰ』教員研修用教材」の「学習16」にある「確定モデルと確率モデル」では確率モデルを使ったシミュレーションの題材として乱数関数を使ったサイコロのプログラムとサイコロ結果の度数分布シミュレーションが紹介されています。こちらの内容をJavaScriptとグラフライブラリのPlotly.jsで学習する方法を紹介いたします。
サンプルプロジェクト
サイコロによる確率モデル(ダイレクトインポート) (zip版)
JavaScriptで乱数を発生させる方法
プログラミング言語ではランダムな値を発生させるための関数が標準機能として搭載されていることが多いです。JavaScriptではMath.random()関数で乱数を発生させることができます。Math.random()は0~0.999…の範囲でランダムな値を返します。なお、乱数にも幾つか種類があるのですが、このような乱数を一様乱数と呼びます。
Math.random()
サイコロ(6面ダイス)のように1~6の範囲で乱数を得たい場合、上記のようなランダム関数があれば実現可能です。
let min = 1;
let max = 6;
let length = max - min + 1;
let value = Math.floor(Math.random() * length) + min;
console.log(value);
まず、サイコロの最小値は1、最大値が6とした場合、6パターンの結果が得られますので(6 – 1 + 1)でlengthを6とします。
次に、Math.random()の値とlengthをかけ算して値を求めます。そして小数点を切り捨てた上で最小値の値を足します(今回は1)。
この計算で本当にサイコロの値を再現できるのか、表にまとめてみました。
| Math.rando()の値 | 6を掛けた値 | 小数点を切り捨てた値 | +1 |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0.1 | 0.6 | 0 | 1 |
| 0.2 | 1.2 | 1 | 2 |
| 0.5 | 3.0 | 3 | 4 |
| 0.9 | 5.4 | 5 | 6 |
確かにサイコロの再現が出来ていることが確認できます。
サイコロを再現する関数の作成
折角なのでサイコロを再現する関数を作ってみます。汎用性を持たせるために引数を指定すれば10面ダイスなどにも対応できるようにしておきます。
function random(min = 1, max = 6) {
let length = max - min + 1;
let value = Math.floor(Math.random() * length) + min;
return value;
}
サイコロを再現する関数の作成(配列版)
文科省の教員研修資料では乱数を沢山生成して配列で取得する関数が使われているため、同様の関数を作成することにします。先ほど作成した関数をループ処理で複数回呼べば実現可能です。
function random_values(min = 1, max = 6, number = 1) {
let result = [];
for (let i = 0; i < number; i++) {
result.push(random(min, max));
}
return result;
}
サイコロ関数の動作確認
console.log(random_values(1, 6, 100));
実行結果(例)
(100) [5, 5, 2, 5, 6, 4, 5, 1, 6, 4, 2, 6, 4, 2, 6, 4, 2, 1, 4, 2, 3, 3, 1, 1, 5, 3, 6, 3, 3, 6, 3, 3, 6, 1, 1, 5, 5, 6, 6, 2, 5, 3, 1, 6, 1, 5, 2, 3, 1, 6, 2, 5, 4, 5, 4, 4, 5, 2, 1, 1, 4, 3, 1, 3, 5, 3, 6, 2, 1, 6, 6, 5, 3, 3, 4, 5, 4, 1, 5, 3, 3, 4, 2, 4, 6, 2, 4, 6, 1, 1, 4, 4, 1, 5, 2, 6, 4, 5, 2, 3]
サイコロの結果を度数分布(棒グラフ)で確認する
1から6の目の出現数が本当にランダムかどうか、度数分布(棒グラフ)で確認してみます。サイコロを振る回数が10回程度だと全部1や6が出る可能性があるため、100回や1000回など、試行回数を増やしながら実験します。
<script src="https://cdn.plot.ly/plotly-latest.min.js"></script>
<script>
function random(min = 1, max = 6) {
let length = max - min + 1;
let value = Math.floor(Math.random() * length) + min;
return value;
}
function random_values(min = 1, max = 6, number = 1) {
let result = [];
for (let i = 0; i < number; i++) {
result.push(random(min, max));
}
return result;
}
function plot() {
let deme = random_values(1, 6, 10000);
let result = {
1:0,
2:0,
3:0,
4:0,
5:0,
6:0
}
for (let i = 0; i < deme.length; i++ ) {
result[deme[i]]++;
}
// グラフ
let graph = "myDiv";
let layout = {
height: 400,
width: 400,
showlegend:false,
title:"サイコロ・シミュレーション",
xaxis: {
title: "出目"
},
yaxis: {
title: "回数"
},
};
let x_memori = ["1","2","3","4","5","6"];
let trace = {
x: x_memori,
y: Object.values(result),
type: "bar"
};
let data = [trace];
Plotly.newPlot(graph, data, layout);
}
</script>
</head>
<body onload="plot()">
<div id="myDiv"></div>
</body>
変数定義
サイコロを100回振った結果をdeme配列に格納します。また、1~6の値が何回ずつ出たのかを集計するための連想配列としてresultを用意します。まずは全部0回として初期化します。
let deme = random_values(1, 6, 100);
let result = {
1:0,
2:0,
3:0,
4:0,
5:0,
6:0
}
ループ処理
出目配列を元にループを行い、1~6の値が何回出たのかをresult連想配列に集計します。
for (let i = 0; i < deme.length; i++ ) {
result[deme[i]]++;
}
グラフ描画
x軸のラベル名を配列で用意しつつ、トレース用の連想配列を用意します。
let x_memori = ["1", "2", "3", "4", "5", "6"];
let trace = {
x: x_memori,
y: Object.values(result),
type: "bar"
};
let data = [trace];
結果
ランダムなので毎回結果は変わりますが、例えば以下のような図がプロットされます。
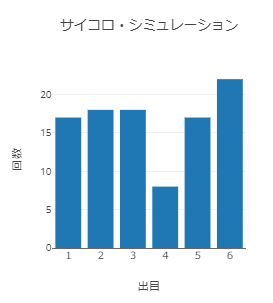
分布が偏っていることが確認できます。
回数を1000や10000などに増やして実験してみてください。
