物体の放物運動のモデル化(斜方投射)

文部科学省発行「高等学校情報科『情報Ⅰ』教員研修用教材」の「学習17」にある「自然現象のモデル化とシミュレーション」では物体の放物運動のモデル化と題して、物体を投げたときの軌跡や距離などを求める「物体の放物運動のモデル化(斜方投射)」が紹介されています。こちらの内容をJavaScriptとグラフライブラリのPlotly.jsで学習する方法を紹介いたします。

サンプルプロジェクト

物体の放物運動のモデル化 (zip)

物体の放物運動のモデル化_関数化バージョン (zip)

完成イメージ

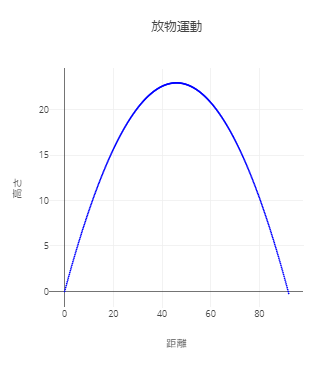
放物運動について考える

まず、放物運動について考えてみることにします。
なお、研修用教材に合わせて単純化のために空気抵抗は省いてモデル化します。

物体を投げたとき、物体は放物線を描くように一定の高さまで上昇し、途中で重力で落下して着地します。強く投げれば初速度も速くなり、高く遠くへ飛ぶはずです。また、角度によっても高やさ飛距離は変わると考えられます。それと、真上に上げた場合には飛距離は0になるはずです。

水平方向(X)の移動(つまり飛距離)

今回は空気抵抗を省いて考えますので、水平方向への移動を妨げるものはありません。等速運動になります。重力によって地面に着地するまでずっと同じスピードで飛んでいきます。

水平方向の速度は「初速度」と「角度」が分かれば三角関数のコサインを使って求められます。コサインはMathの機能で呼び出せるため以下のような記述で求められます。


v0 = 30;  // 初速度
deg = 60; // 角度(deg)
angle = deg * Math.PI / 180.0;  // 投げ上げ角度（ラジアン）
vx = v0 * Math.cos(angle) // 水平「方向」の初速度

「15」という数字が得られました。角度60度で投げると速度は半減するようです。

鉛直方向（Y）の移動

もし空気抵抗だけじゃなくて重力も無視して良いのであれば、ずっと落下せず、投げた方向に等速運動でずっと飛んでいって宇宙の果てまで飛んでいけるのですが、重力があるので徐々に鉛直方向への速度は減少していきます。そして重力に負けて鉛直方向への速度はマイナスになり最後は地面に着地します。

鉛直方向の初速度も「初速度」と「角度」が分かれば三角関数のサインを使って求められます。サインもMathの機能で呼び出せるため以下のような記述で求められます。


v0 = 30;  // 初速度
deg = 60; // 角度(deg)
angle = deg * Math.PI / 180.0;  // 投げ上げ角度（ラジアン）
vy = v0 * Math.sin(angle); // 鉛直「方向」の初速度

「25.980762113533157」という数字が得られました。
角度60度で投げた場合には水平方向の速度より鉛直方向の速度の方がだいぶ速いようですね。

重力加速度の影響

しかし、鉛直方向には重力があります。
地球の重力加速度は9.8m/s²なので1秒ごとに速度が9.8m/s変化します。
約25m/sの速度で「鉛直投げ上げ」した物体は約2.5秒（約25m/s）で落下しはじめます。

ちなみに、初速度30m/sというのは時速に直すと108km/hなので、時速108km・角度60度で投げた球が約2.5秒で地面に落下しはじめ、約5秒後には着地するという話とも言えます。

JavaScriptで物体の放物運動をグラフ化する

今回は変数が沢山登場するため、文科省の研修用教材に倣って変数表を作成します。

変数表

変数名	意味
max	繰り返し上限数。文科省の教員研修資料ではこの値は変数化されておらずコード中に直接1000と指定されている。
dt	時間間隔。文科省版では0.01が代入されている。
v0	初速度。文科省版では30が指定されている。条件を変えてシミュレーションしたいときにはこの値を変えることになる。
g	重力加速度。地球の重力加速度は9.8m/s²なのでこの変数にも9.8m/s²が入る。月の斜方投射をシミュレーションしたいときにはこの値を減らすことになる。
angle	投げ上げ角度をラジアンで代入する。角度60度や45度はラジアンではなくdegなので変換してから代入する必要あり。
x	水平位置。真上や後ろにでも投げない限りは時間とともに増加していく。
y	鉛直位置。投げはじめは上昇を続けるが重力によって途中から下がって最後は地面に着地する。
vx	水平速度。今回の設定では空気抵抗がないことになっているため繰り返し中では一切変化しない。
vy	鉛直速度。最初は整数だが重力加速度により徐々に減少し負数になっても加速し続ける。
vyavg	鉛直速度の「平均」。この値を先に求めないと鉛直位置が求められない。

ソースコード（全体像）


    <script src="https://cdn.plot.ly/plotly-latest.min.js"></script>
    <script>
    function plot() {
        let dt = 0.01; // 微小時間(時間間隔)
        let max = 1000; // ループ上限 
        let v0 = 30; // 初速度
        let g = 9.8; // 重力加速度
        let angle = 45.0 * Math.PI / 180.0;  // 投げ上げ角度（ラジアン）

        let x = [0]; // 水平位置の初期値は0(距離)
        let y = [0]; // 鉛直位置の初期値は0(高さ)
        let vx = [v0 * Math.cos(angle)]; // 水平「方向」の初速度
        let vy = [v0 * Math.sin(angle)]; // 鉛直「方向」の初速度

        let vyavg; // 鉛直方向の平均速度


        console.log("x:" + x , " y:" + y + " vx:" + vx + " vy:" + vy);

        for (let i = 0; i < max; i++) {
            vx.push(vx[i]);
            vy.push(vy[i] - g * dt);
            x.push(x[i] + vx[i] * dt);
            vyavg = (vy[i] + vy[i + 1]) / 2.0;
            y.push(y[i] + vyavg * dt);

            // 高さが0未満になったら終了
            if (y[i] < 0) {
                console.log(i + "回目のループで着地");
                break;
            }
            console.log("x:" + x[i] , " y:" + y[i] + " vx:" + vx[i] + " vy:" + vy[i]);
        }

        // グラフ
        let graph = "myDiv";
        let layout = {
            height: 500,
            width:  500,
            showlegend:false,
            title:"放物運動",
            xaxis: {
                title: "距離"
            },
            yaxis: {
                title: "高さ"
            },
        };
        let trace = {
            x: x,
            y: y,
            mode: "markers",
            type: "scatter",
            marker:{
                color:"blue",
                size:2
            }
        };
        let data = [trace];

        Plotly.newPlot(graph, data, layout);
    }
    </script>
</head>
<body onload="plot()">
    <div id="myDiv"></div>
</body>

変数定義

以下は変数定義部分のソースコードです。ラジアンの計算、水平方向の初速度計算、鉛直方向の初速度計算が含まれています。また、x,y,vx,vyはは時間間隔毎の値を「配列」で記録するため、若干複雑です。


let dt = 0.01; // 微小時間(時間間隔)
let max = 1000; // ループ上限 
let v0 = 30; // 初速度
let g = 9.8; // 重力加速度
let angle = 45.0 * Math.PI / 180.0;  // 投げ上げ角度（ラジアン）

let x = [0]; // 水平位置の初期値は0(距離)
let y = [0]; // 鉛直位置の初期値は0(高さ)
let vx = [v0 * Math.cos(angle)]; // 水平「方向」の初速度
let vy = [v0 * Math.sin(angle)]; // 鉛直「方向」の初速度

let vyavg; // 鉛直方向の平均速度

console.log("x:" + x , " y:" + y + " vx:" + vx + " vy:" + vy);

確認のためにconsole.log()で各値をログに書き出していますので確認してみて下さい。

ループ処理

諸条件を変数で定義したらループ処理で時間間隔毎の物体の位置や加速度を計算します。時間間隔が0.01秒で繰り返し上限が1000なので最大10秒分を計算しますが鉛直位置が0未満になった時点で着地と見なしてループ処理を中断します。


for (let i = 0; i < max; i++) {
    vx.push(vx[i]);
    vy.push(vy[i] - g * dt);
    x.push(x[i] + vx[i] * dt);
    vyavg = (vy[i] + vy[i + 1]) / 2.0;
    y.push(y[i] + vyavg * dt);

    // 高さが0未満になったら終了
    if (y[i] < 0) {
        console.log(i + "回目のループで着地");
        break;
    }
    console.log("x:" + x[i] , " y:" + y[i] + " vx:" + vx[i] + " vy:" + vy[i]);
}

なお着地による中断処理を行わないと、斜方投射した物体が高いところから落下し続ける様子をシミュレーションできます。

水平速度

水平速度の配列に現在の水平速度をそのまま追加します。


vx.push(vx[i]);

鉛直速度

鉛直速度の配列にdt秒後の鉛直速度を追加します。


vy.push(vy[i] - g * dt);

つまり「9.8m * 0.01 ≒ 0.1」速度が減ります。

水平位置

水平位置の配列にdt秒後の水平位置を計算して追加します。


x.push(x[i] + vx[i] * dt);

水平方向に秒速15mで進んでいたとしたらdtは0.01秒なので0.15m移動した距離が追加されます。

鉛直位置

鉛直位置の配列にdt秒後の鉛直位置を追加します。


vyavg = (vy[i] + vy[i + 1]) / 2.0;
y.push(y[i] + vyavg * dt);

鉛直方向の速度はdt秒毎に変化しているため、鉛直位置の計算をするためには平均速度を求める必要があります。平均速度を求める式は以下の通りです。

平均速度＝（現在の速度　＋　微小時間後の速度）／２

平均速度さえ求められれば、あとは水平位置の計算と同じです。

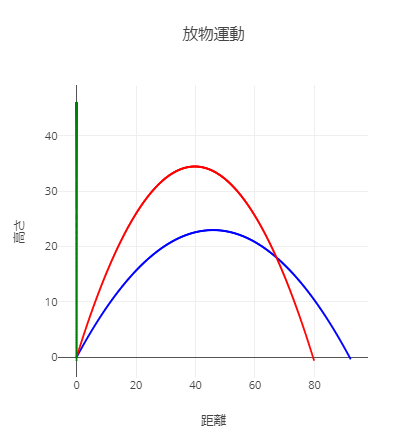
複数の角度でグラフを描いて比較する

一番遠くに飛ぶ角度と一番高く飛ぶ角度を求めようという演習が教員研修資料では示されています。
複数のグラフを描画するためにコピペで対応すると可読性や保守性が悪くなるので、先にプログラムを改造してシミュレーション部分を「関数化」してから描画してみることにします。

シミュレーション部分の関数化

放物運動の初速度と角度とグラフの色を引数で指定できる関数を作成します。また、返り値でグラフ描画ライブラリが必要とする情報を返せるようにします。
※ 引数を省略したときには適当な初速度と角度と色を適応するようにしています。


function simulation (v0 = 30, deg = 45, color = "blue") {
    let dt = 0.01; // 微小時間(時間間隔)
    let max = 1000; // ループ上限 
    let g = 9.8; // 重力加速度
    let angle = deg * Math.PI / 180.0;  // 投げ上げ角度（ラジアン）
    let x = [0]; // 水平位置の初期値は0(距離)
    let y = [0]; // 鉛直位置の初期値は0(高さ)
    let vx = [v0 * Math.cos(angle)]; // 水平「方向」の初速度
    let vy = [v0 * Math.sin(angle)]; // 鉛直「方向」の初速度
    let vyavg; // 鉛直方向の平均速度

    console.log("x:" + x , " y:" + y + " vx:" + vx + " vy:" + vy);

    for (let i = 0; i < max; i++) {
        vx.push(vx[i]);
        vy.push(vy[i] - g * dt);
        x.push(x[i] + vx[i] * dt);
        vyavg = (vy[i] + vy[i + 1]) / 2.0;
        y.push(y[i] + vyavg * dt);

        // 高さが0未満になったら終了
        if (y[i] < 0) {
            console.log(i + "回目のループで着地");
            break;
        }
        console.log("x:" + x[i] , " y:" + y[i] + " vx:" + vx[i] + " vy:" + vy[i]);
    }

    let trace = {
        x: x,
        y: y,
        mode: "markers",
        type: "scatter",
        marker:{
            color:color,
            size:2
        }
    };

    return trace;
}

グラフ描画部分の関数

放物運動の計算をシミュレーション関数に任せることにしたのでグラフ描画部分は非常に簡単になります。


function plot() {
    let graph = "myDiv";   
    let data = [
        simulation(30, 45, "blue"),
        simulation(30, 60, "red"),
        simulation(30, 90, "green"),
    ];
    let layout = {
        height: 500,
        width:  500,
        showlegend:false,
        title:"放物運動",
        xaxis: {
            title: "距離"
        },
        yaxis: {
            title: "高さ"
        },
    };

    Plotly.newPlot(graph, data, layout);
}

具体的には以下の部分でシミュレーション関数を呼び出しています。


let data = [
    simulation(30, 45, "blue"),
    simulation(30, 60, "red"),
    simulation(30, 90, "green"),
];

これなら3個でも4個でも、簡単にトレースするグラフを増やせますね。