文部科学省発行「高等学校情報科『情報Ⅰ』教員研修用教材」の「学習16」にある「確定モデルと確率モデル」では確率モデルを使ったシミュレーション手法としてモンテカルロ法による円周率の計算が紹介されています。こちらの内容をJavaScriptとグラフライブラリのPlotly.jsで学習する方法を紹介いたします。
サンプルプロジェクト
モンテカルロ法による円周率計算(グラフなし) (zip版)
モンテカルロ法による円周率計算(グラフあり) (zip版)
その前に、まず、円周率の復習から説明いたします。
円周率とはなんぞや?
円の面積や円の円周の長さを求めるときに使う、3.14…の数字です、π(パイ)のことです。
πは数学定数の一つだそうです。JavaScriptではMathオブジェクトのPIプロパティで円周率を取ることができます。
alert(Math.PI)
正方形の四角形の面積と円の面積
正方形の四角形の面積は縦と横の長さが分かれば求められます。
上記の図は縦横100pxの正方形です。
正方形の面積 = 縦 * 横
100 * 100 = 10000です。
次に円の面積を求めてみましょう。
こちらの円は直径100pxの円です、半径は50です。半径のことを「r」と呼びますね。
円の面積 = 半径 * 半径 * π
πの近似値を「3」とした場合
50 * 50 * π = 2500π ≒ 7500 です。
当たり前ですが正方形の方が円よりも面積が大きいことが分かります。図で表してみましょう。
どうやって円周率を求めるか?
まず、円の中心から円周に向かって線を何本か引いてみます。
この線は中心から見た場合、半径の長さであり、今回の場合は「50」です。
次に、中心から90度分、四角と円を切り出した次の図形を見て下さい。
モンテカルロ法による円周率の計算では、この図に乱数で点を打つ
上記の図に対して沢山の点をランダムに打ちます、そして円の面積に落ちた点の数を数えることで円周率が求まります!
試しにx:30,y:30の位置に点をプロットしてみます、見やすいようにちょっと大きめの点にしますが、1pxの点ということで脳内で補正して頂けると幸いです。
円の内側にプロット
この点は図で見ると明らかに円の面積の中に収まっていますが、念のため計算で円の中に入っているか確認します。
中心から点がどれくらい離れているのかを以下の数式で求めます。
横の長さ(x)の二乗 + 縦の長さ(y)の二乗 = 距離の二乗
(30 * 30) + (30 * 30) = 900 + 900 = 1800
これは三平方の定理です。
1800の平方根を求めれば距離も求められますが、距離の比較ができれば二乗されていても構わないので放っておくことにします。
今度は円の外の点も試してみます、x:40,y:40の位置でどうでしょう。
円の外にプロット
(40 * 40) + (40 * 40) = 1600 + 1600 = 3200
1800はOKで3200はNGのようです。
実は円の中に収まる距離とはみ出る距離の境目は、半径から求められます。
半径の二乗以下なら円の中と見なすことができます。
半径の二乗 = 50 * 50 = 2500
円の中心から一番遠いところにプロット
因みに、一番遠いところは右上の隅です。
距離は(50 * 50) + (50 +* 50) = 5000で、やはり円の外となります。
JavaScriptでモンテカルロ法による円周率計算を行う
文科省の「情報Ⅰ」教員研修資料に掲載されているコードを参考にJavaScriptで円周率の近似値を求めてみます。
※文科省の資料では図のサイズが縦横は50ではなく1.0ですので、以下、縦横のサイズは1.0とします。
// 計算に使う変数の定義
let totalcount = 10000;
let incount = 0;
let x,y,distance,pi;
// ランダムにプロットしつつ円の中に入った数を記録
for (let i = 0; i < totalcount; i++) {
x = Math.random();
y = Math.random();
distance = x ** 2 + y ** 2;
if (distance < 1.0){
incount++;
}
console.log("x:" + x + " y:" + y + " D:" + distance);
}
// 円の中に入った点の割合を求めて4倍する
pi = (incount / totalcount) * 4;
document.write("円周率は" + pi);
実行結果
円周率は3.146
解説
変数定義
1~4行目は計算に使う変数を定義しています。
変数totalcountではランダムにプロットする回数を宣言しています。
10000回ぐらいプロットすると3.14に近い数字が出てきます。1000回ぐらいですと結構ズレますので、実際に試してください。
プロットし続ける
7行目の繰り返し文では乱数を使って点をプロットし、円の中に収まったらincount変数をインクリメントしています。
8~9行目では点の位置x,yの値を乱数で求めています。乱数の取得はプログラミング言語が備えている乱数命令で行えます。JavaScriptの場合はMath.random()命令で求められます。この命令は0以上1未満の小数をランダムに返してくれます(0 - 0.999~)。
点の位置が決まったら、円の中心から点の位置までの距離を求めます。距離はx二乗 + y二乗で求められます。
仮にxとyの値が両方とも0.5ならば0.25 + 0.25 = 0.5となります。
12行目のif文では円の中に収まっているかどうかの判定を行っています。点の位置であるx,yの値を二乗して加算した値がrの二乗よりも小さければOKです。今回の円はrが1.0なので二乗しても1.0です。
仮に距離が0.5だったばあいは1.0よりも小さいので円の中です。距離が1.0を越えるためには、xやyの値が0.8ぐらい必要です。
ループ毎のxやyやdistanceの値はconsole.log()でログを残しておりますので、デバッグツールを使えば確認できるようにしてあります。
プロット数から円周率を求める
19行目では円の中に入った点の割合を求め、それを4倍にすることで円周率を求めています。今回の計算で使っている円が正円ではなくて四半円なので4倍する必要があります。
※(半径が1なので、 四半円の面積が 1 * 1 * pi / 4 になり、その4倍だから)
今回の実行結果は3.146になりましたが、プロットの回数が少ないとブレます。
JavaScriptとPlotly.jsでモンテカルロ法による円周率の計算を散布図で確認
上記のプログラムを散布図のグラフにすると以下のようになります。
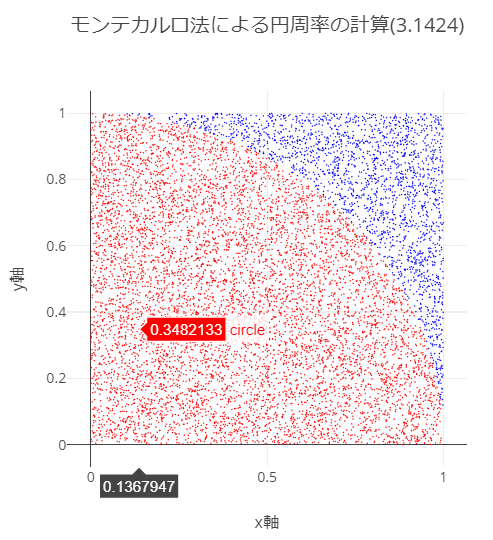
ソースコード
グラフライブラリの読み込みやラベル名の設定などがあるためちょっと長くなりますが、モデル化の部分のコードは先ほどと、殆ど変わりません。
<script src="https://cdn.plot.ly/plotly-latest.min.js"></script>
<script>
function plot() {
// 計算に使う変数の定義
let totalcount = 10000;
let incount = 0;
let x, y, distance, pi;
let circle_x = [];
let circle_y = [];
let outer_x = [];
let outer_y = [];
for (var i = 0; i < totalcount; i++) {
x = Math.random();
y = Math.random();
distance = x ** 2 + y ** 2;
if (distance < 1.0 ** 2){
incount++;
circle_x.push(x);
circle_y.push(y);
} else {
outer_x.push(x);
outer_y.push(y);
}
console.log("x:" + x + " y:" + y + " D:" + distance);
}
// 円の中に入った点の割合を求めて4倍する
pi = (incount / totalcount) * 4;
console.log("円周率は" + pi);
// 計算した値をグラフ用の変数に格納して描画
let graph = "myDiv";
let layout = {
height: 500,
width: 500,
showlegend:false,
title:"モンテカルロ法による円周率の計算(" + pi + ")",
xaxis: {
title: 'x軸'
},
yaxis: {
title: 'y軸'
},
};
let circle = {
x: circle_x,
y: circle_y,
name:"circle",
mode: 'markers',
type: 'scatter',
marker:{
color:'red',
size:1
}
};
let outer = {
x: outer_x,
y: outer_y,
name:"outer",
mode: 'markers',
type: 'scatter',
marker:{
color:'blue',
size:1
}
};
let data = [circle,outer];
Plotly.newPlot(graph, data, layout);
}
</script>
</head>
<body onload="plot()">
<div id="myDiv"></div>
</body>
プロットするたびに位置を配列に記録する
前回のプログラムとの違いは、プロットするたびに位置を配列に記録していることです。
円の面積に収まっているときはcircle_xとcircle_yに位置を記録し、円の外の場合はouter_xとouter_yに記録をしています。
if (distance < 1.0 ** 2){
incount++;
circle_x.push(x);
circle_y.push(y);
} else {
outer_x.push(x);
outer_y.push(y);
}
グラフのレイアウト
グラフのタイトルを付けたり横軸や縦軸のメモリのタイトルを付けたりします。また、図のサイズを大きめの正方形にしたいので高さ500、横幅500に設定します。
let layout = {
height: 500,
width: 500,
showlegend:false,
title:"モンテカルロ法による円周率の計算(" + pi + ")",
xaxis: {
title: 'x軸'
},
yaxis: {
title: 'y軸'
},
};
円の中に収まっているときのグラフ
circle_xとcircle_yの値を元にグラフを用意します。点の色やサイズを決めたり、名前を定義できます。
let circle = {
x: circle_x,
y: circle_y,
name:"circle",
mode: 'markers',
type: 'scatter',
marker:{
color:'red',
size:1
}
};
円の外側のグラフも定義しますが、中身があまり変わらないため解説は省略します。
プロットする
グラフ用のデータが揃ったらplot命令で図をプロットします。
let data = [circle,outer];
Plotly.newPlot(graph, data, layout);
