文部科学省発行「高等学校情報科『情報Ⅰ』教員研修用教材」の「学習16」にある「確定モデルと確率モデル」では確定モデルを使ったシミュレーションの題材として複利法による預金の複利計算が紹介されています。こちらの内容をJavaScriptとグラフライブラリのPlotly.jsで学習する方法を紹介いたします。
完成イメージ
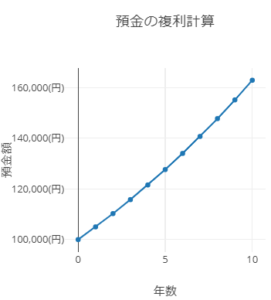
サンプルプロジェクト
複利とは何か
10万円の預金を年利5%で運用した場合、1年後には10.5万円になります。利息は0.5万円です。この利息を趣味などで消費した場合は来年の利息も同じになりますが、使わずに預けた場合には0.5万円の分にも利息が付きます。そのため翌年の利息は5,250円となります。
利息を再投資する場合を複利、しないのを単利と呼びます。単利だと5%の利息で預金を倍にするためには20年の運用が必要となりますが、複利なら17年ぐらいで倍にできます。
凄いですね、「複利は人類最大の発明」と、かのアインシュタインが言ったそうです(本当かなぁ)。
プログラミングで複利計算をする
10万円の預金を年利5%の複利で運用した場合の金額だけであれば、複利終価係数という式を使えば電卓でも求められますが、プログラムを書けば毎年どれくらい増えていくのかを文字で出力したりグラフで表示することもできます。
let yokin = 100000;
let riritsu = 0.05;
let risoku;
let term = 10;
for (let i = 0; i < term; i++) {
risoku = yokin * riritsu;
yokin = yokin + risoku;
document.write(i + 1, "年目:", yokin, "
");
}
実行結果
1年目:105000
2年目:110250
3年目:115762.5
4年目:121550.625
5年目:127628.15625
6年目:134009.5640625
7年目:140710.042265625
8年目:147745.54437890626
9年目:155132.82159785158
10年目:162889.46267774416
解説
とりあえず10年で16万2889円になりました。
余談:終価係数で求めてみる
ちなみに10年5%の終価係数を計算で求めると以下のような式になります。
終価係数 = (1 + 0.05)¹⁰
手近な関数電卓で叩いてみましょう。
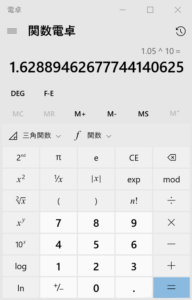
この係数を10万円の元本に掛け合わせると、最終的な結果は殆ど同じですね。
預金の複利計算をグラフで表示する
毎年の預金額を配列に記録していけばグラフで資産の上昇具合を視覚的に確認できます。
<script src="https://cdn.plot.ly/plotly-latest.min.js"></script>
<script>
function plot() {
let yokin = [100000];
let riritsu = 0.05;
let risoku;
let term = 10;
for (let i = 0; i < term; i++) {
risoku = yokin[i] * riritsu;
yokin.push(yokin[i] + risoku);
}
// グラフ
let graph = "myDiv";
let layout = {
height: 400,
width: 400,
showlegend:false,
title:"預金の複利計算",
xaxis: {
title: "年数"
},
yaxis: {
title: "預金額",
ticksuffix:"(円)",
exponentformat:"none",
},
};
let trace = {
y: yokin,
mode: 'lines+markers',
type: 'scatter'
};
let data = [trace];
Plotly.newPlot(graph, data, layout);
}
</script>
</head>
<body onload="plot()">
<div id="myDiv"></div>
</body>
変数定義
預金の初期値を配列で持つことが前回との違いです。
let yokin = [100000];
let riritsu = 0.05;
let risoku;
let term = 10;
ループ部分
現在の預金(1回目のループなら10万円が入っている)を元に、次の年の預金額を求めて配列に追加します。
for (let i = 0; i < term; i++) {
risoku = yokin[i] * riritsu;
yokin.push(yokin[i] + risoku);
}
push()は配列に要素を追加する命令です。現在の預金に利息を追加して配列を追加しているわけです。
なお、「学習16」と「学習17」では、このように現在の値を元に配列の値を追加していくパターンのプログラムが続きますので、比較的簡単な今回の「預金の複利計算」で馴れておかれることを強くお勧めします。
グラフの設定
横軸が年数で縦軸が預金額です。分かりやすいように(円)というメモリのサフィクスも追加します。それと、桁の大きい数字をグラフライブラリに渡すと数字が接頭辞表記になってしまうので、「exponentformat:"none"」と記述して止めます。
xaxis: {
title: "年数"
},
yaxis: {
title: "預金額",
ticksuffix:"(円)",
exponentformat:"none",
},
グラフの種類は散布図で、マーカーとラインがついたものにします。x軸は0年から1づつ増えるタイプなのでy軸の値を配列で渡せば省略可能です。
let trace = {
y: yokin,
mode: 'lines+markers',
type: 'scatter'
};
演習:パラメーターを変更しながら利息計算の特徴について考える
30年ぐらい運用すると以下のようなグラフになります。
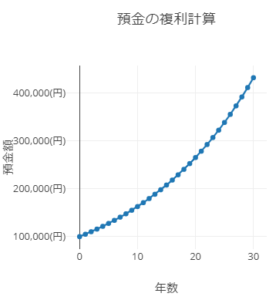
つまり、資産形成は若いうちから行いましょうという、ファイナンシャルプランナーが言いそうな結果になります。
また、利息が5%ではなく10%ですと、凄い勢いで預金が膨れ上がります。
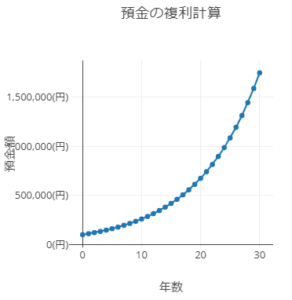
10万円が30年で150万円越えになりました。15倍以上です。
これが預金なら良いのですが、10%の利息が付く預金は今時はありません。どちらかというと、借金の利息なら10%というのは十分あり得ます。利息が返せないと複利効果でエラいことになります。この図から得られる教訓は、借金には気をつけようということです。
おわりに
複利計算のプログラムは授業でも扱いやすいネタです。「きのくにICT教育」でも複利計算のサンプルアプリを使っております。また、改造のバリエーションとして「積立貯金」は分かりやすいテーマです。複利を効かせつつ、毎年10万円ずつ積み立てた場合には10年でどれくらい資産形成を行えるか、といったお題を出すことができます。積立の場合は「年金終価係数」でも確認できるので、値が正しいかを確認するときに「年金終価係数」の値と比較するのも良いと思います。
また、借金返済のシミュレーションはテーマが重たいですが、改造パターンとしては挑戦しやすいです。実際に研修で扱ったこともございます。
